DirectX11의 공부 목적으로 위 링크의 튜토리얼을 보고 제 생각을 포함하여 정리하였습니다.

들어가며

win api를 자세히 보기보다 렌더링 부분을 먼저 공부 하고 싶기 때문에 지금 시간인 세팅 부분은 간단하게 넘어가려한다.

● 프로젝트 생성시 'win32 console applicaiton' 는 'windows desktop application' 으로 변경 되었다.

프레임 워크는 네 클래스로 시작된다.

1. 앱의 진입점인 WinMain 함수

2. WinMain의 기능을 캡슐화한 SystemClass

3. 사용자의 키보드 입력을 처리하기 위한 InputClass

4. DirectX의 그래픽 코드를 처리하기 위한 ApplicationClass

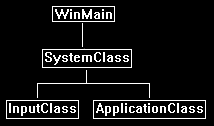
이 네 클래스를 자세히 살펴보겠습니다.

main.cpp

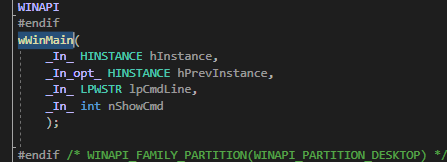
내가 사용하는 vs에서는 WinMain이  APIENTRY wWinMain으로 생성되었었다.

기본 WinMain과 큰 차이는 없지만 튜토리얼과 같이 WinMain함수로 변경하여 간단하게 만들고 메인작업들을 System class를 이용해 캡슐화하여 사용한다.

WinMain vs wWinMain

#include "systemclass.h"

int WINAPI WinMain(_In_ HINSTANCE hInstance, _In_opt_ HINSTANCE hPrevInstance,	_In_ LPSTR lpCmdLine, 	_In_ int nShowCmd
)
{
	SystemClass* System;
	bool result;

	// 새로운 개체 생성.
	System = new SystemClass;

	// System 개체 초기화 후 실행.
	result = System->Initialize();
	if (result)
	{
		System->Run();
	}

	// System 개체 종료 후 메모리 해제
	System->Shutdown();
	delete System;
	System = 0;

	return 0;
}

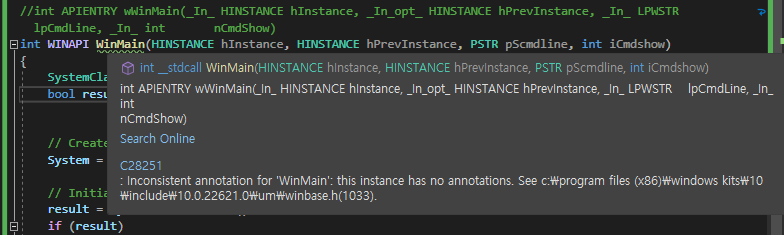
튜토리얼의 코드대로 작성하게 되면 이런 경고가 나오는데, 이는 주석 코드(SAL)이 없기 때문에 발생한 경고다.

WinMain의 함수 정의에 SAL이 사용되었기 때문에 정의에서도 사용해주어야 한다.

System.h

#ifndef _SYSTEMCLASS_H_
#define _SYSTEMCLASS_H_

// 암호화, DDE, RPC, 셸 및 Windows 소켓과 같은 API를 제외 하여 빌드 프로세스 속도를 향상
#define WIN32_LEAN_AND_MEAN

// win32 함수를 사용하려는 목적인 windows.h 포함
#include <windows.h>
#include "inputclass.h"
#include "applicationclass.h"

class SystemClass
{
public:
	SystemClass();
	SystemClass(const SystemClass&);
	// 소멸자가 호출되지 않을 수도 있는 경우가 있기 때문에 소멸 작업은 Shutdown함수에 구현.
	// 그래서 기본 소멸자에 아무것도 없으므로 default 사용
	~SystemClass() = default;

	bool Initialize();
	void Shutdown();
	void Run();

	// Windows 시스템 메시지를 처리하기 위한 핸들
	LRESULT CALLBACK MessageHandler(HWND, UINT, WPARAM, LPARAM);

private:
	// 실질적으로 매 프레임마다 앱의 처리를 담당
	bool Frame();
	// 앱의 초기화 작업
	void InitializeWindows(int&, int&);
	// 앱의 종료시 작업
	void ShutdownWindows();

private:

	LPCWSTR m_applicationName;
	HINSTANCE m_hinstance;
	HWND m_hwnd;

	// 우리가 만든 클래스
	InputClass* m_Input;
	ApplicationClass* m_Application;
};


static LRESULT CALLBACK WndProc(HWND, UINT, WPARAM, LPARAM);
static SystemClass* ApplicationHandle = 0;

#endif

WinMain의 작업들을 캡슐화하기 위한 클래스.

처음의 WIN32_LEAN_AND_MEAN은 빌드시 암호화, DDE, RPC, 셸 및 Windows 소켓과 같은 API를 제외 하여 빌드 프로세스 속도를 향상시켜준다.

System.cpp

1. 생성자

SystemClass::SystemClass()
{
	// 우리가 만든 클래스의 개체
	m_Input = nullptr;
	m_Application = nullptr;
}

생성자는 개체의 초기화만 들어있다. 응용 프로그램에서는 개체가 null이 아니면 해당 개체를 정리하려고 시도한다고 하는데 이는 쓰레기 값이 들어지 않게 하려는 의도인거 같다.

또한 응용 프로그램에서는 모든 포인터와 변수를 null로 초기화 하지 않으면 일부 릴리즈 빌드가 실패할수 있다고 한다.

나는 보다 명확한 nullptr으로 초기화 하였다.

2. 소멸자

빈 소멸자이기에 코드는 없다. 소멸자가 호출되지 않을 수도 있는 경우가 있기 때문에 소멸시 작업은 모두 Shoutdown함수에 구현되었다.

3. Initialize

bool SystemClass::Initialize()
{
	int screenWidth, screenHeight;
	bool result;

	screenWidth = 0;
	screenHeight = 0;

	// windows api 초기화.
	InitializeWindows(screenWidth, screenHeight);

	// m_Input은 사용자의 키보드 입력을 처리하는데 사용된다.
	m_Input = new InputClass;
	m_Input->Initialize();

	// m_Application은 모든 그래픽 렌더링을 처리한다.
	m_Application = new ApplicationClass;
	result = m_Application->Initialize(screenWidth, screenHeight, m_hwnd);
	if (!result)
	{
		return false;
	}
	return true;
}

평범한 초기화 함수.

4. Shoutdown

void SystemClass::Shutdown()
{
	// 클래스 개체들을 메모리 해제.
	{
		if (m_Application)
		{
			m_Application->Shutdown();
			delete m_Application;
			m_Application = 0;
		}

		if (m_Input)
		{
			delete m_Input;
			m_Input = 0;
		}
	}

	// 창 종료
	ShutdownWindows();

	return;
}

모든 개체를 메모리 해제 후 창을 종료한다.

5. Run

함수 Run의 수도 코드와 실제 코드이다.

while ( 실행중 )
    1. Windows 시스템 메시지 확인 
    2. 시스템 메시지 처리 
    3. 응용 프로그램 루프 
    4. 프레임 처리 (처리 중에 사용자가 종료하기를 원하는지 확인)

void SystemClass::Run()
{
	MSG msg;
	bool done, result;


	// 메세지 구조 초기화
	ZeroMemory(&msg, sizeof(MSG));

	// 창이나 사용자로부터 종료 메세지가 나타날 때까지 반복한다.
	// done이 true면 앱의 종료라는 뜻이다.
	done = false;
	while (!done)
	{
		// 윈도우 메세지의 처리
		if (PeekMessage(&msg, NULL, 0, 0, PM_REMOVE))
		{
			TranslateMessage(&msg);
			DispatchMessage(&msg);
		}

		// Window가 앱을 종료하라는 신호를 보내면 종료한다.
		if (msg.message == WM_QUIT)
		{
			done = true;
		}
		else
		{
			// 종료 신호가 아니라면 프레임 처리를 수행한다.
			result = Frame();
			if (!result)
			{
				done = true;
			}
		}

	}

	return;
}

Run 함수는 애플리케이션이 반복되고 모든 애플리케이션의 처리를 수행하는 곳이다. 실질적으로 애플리케이션의 처리는 Frame함수에서 하게 된다.

6. Frame

프레임마다 그래픽 작업을 수행하는 함수

bool SystemClass::Frame()
{
	bool result;

	// 사용자가 ESC를 누르고 앱을 종료하려고하는지 확인.
	if (m_Input->IsKeyDown(VK_ESCAPE))
	{
		return false;
	}

	// Application 개체를 이용하여 프레임의 그래픽 작업을 수행한다.
	result = m_Application->Frame();
	if (!result)
	{
		return false;
	}

	return true;
}

7. MessageHandler

MessageHandler 함수는 Windows 시스템 메세지를 가져와 전달하는 함수

LRESULT CALLBACK SystemClass::MessageHandler(HWND hwnd, UINT umsg, WPARAM wparam, LPARAM lparam)
{
	switch (umsg)
	{
		// 키보드에서의 키가 눌렸는지 확인.
		case WM_KEYDOWN:
		{
			// 키를 누르면 해당 상태를 저장할 수 있도록 Input개체에 전송한다.
			m_Input->KeyDown((unsigned int)wparam);
			return 0;
		}

		// 키보드에서 키가 해제되었는지 확인.
		case WM_KEYUP:
		{
			m_Input->KeyUp((unsigned int)wparam);
			return 0;
		}

		// 앱에서 사용하지 않는 다른 메세지는 기본 WinAPI메세지 핸들러로 전송한다.
		default:
		{
			return DefWindowProc(hwnd, umsg, wparam, lparam);
		}
	}
}

여기서 우리는 관심 있는 특정 메세지만을 Input 개체에 전송한다. 우리가 필요없는 다른 메세지는 기본 Windows 메세지 핸들러로 전송한다.

8. InitializeWindows

렌더링에 사용할 창을 빌드하기 위한 함수

void SystemClass::InitializeWindows(int& screenWidth, int& screenHeight)
{
	WNDCLASSEX wc;
	DEVMODE dmScreenSettings;
	int posX, posY;


	// System클래스의 포인터를 가져온다.
	ApplicationHandle = this;

	// HInstance는 앱(프로그램)의 핸들을 말한다. 운영체제가 제공해주는 핸들을 GetModuleHandle을 통해 가져온다.
	m_hinstance = GetModuleHandle(NULL);

	// 앱의 이름을 작성.
	m_applicationName = L"Engine";

	// 윈도우 클래스의 변수들을 작성한다. (앱의 창 크기, 앱의 핸들, ...)
	wc.style = CS_HREDRAW | CS_VREDRAW | CS_OWNDC;
	wc.lpfnWndProc = WndProc;
	wc.cbClsExtra = 0;
	wc.cbWndExtra = 0;
	wc.hInstance = m_hinstance;
	wc.hIcon = LoadIcon(NULL, IDI_WINLOGO);
	wc.hIconSm = wc.hIcon;
	wc.hCursor = LoadCursor(NULL, IDC_ARROW);
	wc.hbrBackground = (HBRUSH)GetStockObject(BLACK_BRUSH);
	wc.lpszMenuName = NULL;
	wc.lpszClassName = m_applicationName;
	wc.cbSize = sizeof(WNDCLASSEX);

	// 위에서 작성한 설정 값을 등록한다.
	RegisterClassEx(&wc);

	// 사용자의 모니터 해상도를 가져온다.
	screenWidth = GetSystemMetrics(SM_CXSCREEN);
	screenHeight = GetSystemMetrics(SM_CYSCREEN);

	// 전체 화면으로 실행하는지, 창 모드로 실행하는지에 따라 화면 설정을 설정합니다. 
	if (FULL_SCREEN)
	{
		// 전체 화면인 경우 화면을 사용자 데스크톱의 최대 크기 및 32비트로 설정합니다. 
		memset(&dmScreenSettings, 0, sizeof(dmScreenSettings));
		dmScreenSettings.dmSize = sizeof(dmScreenSettings);
		dmScreenSettings.dmPelsWidth = (unsigned long)screenWidth;
		dmScreenSettings.dmPelsHeight = (unsigned long)screenHeight;
		dmScreenSettings.dmBitsPerPel = 32;
		dmScreenSettings.dmFields = DM_BITSPERPEL | DM_PELSWIDTH | DM_PELSHEIGHT;

		// 디스플레이 세팅을 전체 화면으로 변경한다.
		ChangeDisplaySettings(&dmScreenSettings, CDS_FULLSCREEN);

		// 창의 위치를 왼쪽 상단으로 설정한다.
		posX = posY = 0;
	}
	else
	{
		// 창 모드인 경우 해상도를 800x600으로 설정합니다. 
		screenWidth = 800;
		screenHeight = 600;

		// 창을 화면 중앙에 배치하게끔 왼쪽 상단 position을 구하여 설정한다.
		posX = (GetSystemMetrics(SM_CXSCREEN) - screenWidth) / 2;
		posY = (GetSystemMetrics(SM_CYSCREEN) - screenHeight) / 2;
	}

	// 화면 설정으로 창을 만들고 이에 대한 핸들을 가져온다.
	m_hwnd = CreateWindowEx(WS_EX_APPWINDOW, m_applicationName, m_applicationName,
		WS_CLIPSIBLINGS | WS_CLIPCHILDREN | WS_POPUP,
		posX, posY, screenWidth, screenHeight, NULL, NULL, m_hinstance, NULL);

	// 창을 띄워 메인 포커스로 설정한다.
	ShowWindow(m_hwnd, SW_SHOW);
	SetForegroundWindow(m_hwnd);
	SetFocus(m_hwnd);

	// 마우스 커서를 숨긴다.
	ShowCursor(false);

	return;
}

. 주석으로 어떤 역할인지 알기 쉽다. FULL_SCREEN 전역 변수는 Application class에 있는데 이는 나중에 이해가 될 것이라 한다.

9. ShoutdownWindows

화면 설정을 다시 정상으로 되돌리고 창과 관련된 핸들을 해제하는 함수.

void SystemClass::ShutdownWindows()
{
	// Show the mouse cursor.
	ShowCursor(true);

	// 전체 화면을 종료하는 경우 디스플레이 설정을 수정한다.
	if (FULL_SCREEN)
	{
		ChangeDisplaySettings(NULL, 0);
	}

	// Remove the window.
	DestroyWindow(m_hwnd);
	m_hwnd = NULL;

	// Remove the application instance.
	UnregisterClass(m_applicationName, m_hinstance);
	m_hinstance = NULL;

	// Release the pointer to this class.
	ApplicationHandle = NULL;

	return;
}

10. WndProc

Windows가 메세지를 보내는 함수

LRESULT CALLBACK WndProc(HWND hwnd, UINT umessage, WPARAM wparam, LPARAM lparam)
{
	switch (umessage)
	{
		// Check if the window is being destroyed.
		case WM_DESTROY:
		{
			PostQuitMessage(0);
			return 0;
		}

		// Check if the window is being closed.
		case WM_CLOSE:
		{
			PostQuitMessage(0);
			return 0;
		}

		// 다른 메세지는 System 클래스의 MessageHandler 함수로 전달된다.
		// 이곳으로 메세지가 들어오는 이유는 Initialize 함수에서 wc.lpfnWndProc = WndProc으로 지정했기 때문.
		default:
		{
			return ApplicationHandle->MessageHandler(hwnd, umessage, wparam, lparam);
		}
	}
}

InputClass.h

사용자의 키보드 입력을 처리하는 클래스.

이러한 입력처리는 DirectInput이 더 우수하지만 튜토리얼을 단순하게 유지하기 위해 사용.

아까 보았던 SystemClass::MessageHandler 함수에서 이 InputClass 개체로 메세지를 전달해준다.

#pragma once
#ifndef _INPUTCLASS_H_
#define _INPUTCLASS_H_

class InputClass
{
public:
	// 빈 생성자, 빈 소멸자이기에 default를 사용했다.
	InputClass() = default;
	InputClass(const InputClass&);
	~InputClass() = default;

	void Initialize();

	void KeyDown(unsigned int);
	void KeyUp(unsigned int);

	bool IsKeyDown(unsigned int);

private:
	bool m_keys[256];
};

#endif

키의 저장은 m_keys라는 배열에 저장하게 되고 키에 대한 쿼리를 받으면 그 키에 대한 index를 찾아 호출 기능에 알려주는 형식이다.

InputClass.cpp

간단한 cpp 파일

#include "InputClass.h"

InputClass::InputClass(const InputClass& other)
{
}

void InputClass::Initialize()
{
	// 키의 값을 누르지 않은 뜻인 false로 모두 초기화
	for (int i = 0; i < 256; i++)
	{
		m_keys[i] = false;
	}

	return;
}


void InputClass::KeyDown(unsigned int input)
{
	// If a key is pressed then save that state in the key array.
	m_keys[input] = true;
	return;
}


void InputClass::KeyUp(unsigned int input)
{
	// If a key is released then clear that state in the key array.
	m_keys[input] = false;
	return;
}


bool InputClass::IsKeyDown(unsigned int key)
{
	// 키가 눌렸는지, 눌리지 않았는지의 상태를 반환한다.
	return m_keys[key];
}

ApplicationClass.h

앱의 모든 그래픽 기능은 이 클래스에 캡슐화되어 사용된다. 또한 해상도 변경 등 모든 그래픽 관련 전역 설정에 대해 이 파일의 헤더를 사용할 것이다.

향후 튜토리얼의 모든 그래픽 개체를 포함하게 된다.

#pragma once
#ifndef _APPLICATIONCLASS_H_
#define _APPLICATIONCLASS_H_

#include <windows.h>

const bool FULL_SCREEN = false;
const bool VSYNC_ENABLED = true;
const float SCREEN_DEPTH = 1000.0f;
const float SCREEN_NEAR = 0.3f;

class ApplicationClass
{
public:
	ApplicationClass();
	ApplicationClass(const ApplicationClass&);
	~ApplicationClass();

	bool Initialize(int, int, HWND);
	void Shutdown();
	bool Frame();

private:
	bool Render();

private:
};
#endif

Application.cpp

지금 시간에서는 별다를게 없어 모두 비워져 있다!

요약

기본적인 프레임워크를 구성하고 앱의 창을 띄웠다.

주석만 따라간다면 크게 어려운것은 없었다.

||문제 이해

6
1  2
3  7  4
9  4  1  7
2  7  5  9  4

과 같은 형태의 삼각형이 주어지며 맨 위에서 한번에 한칸씩 내려갈 수 있다.

내려가는 방향은 바로 아래와 그 한칸 오른쪽으로 내려갈 수 있으며

모든 경로중 최대값을 구하라.

||해결 계획

이번 포스팅은 

문제를 보면서 "이렇게 생각을 전개해 나가면 좋겠다라고" 정리한 걸 중심으로 작성하겠다.

완전탐색

1. 답이 최대 합을 출력하라니까 일단 최대 합을 반환하는 함수형태를 만든다.

2. 좀 더 디테일하게 추가 해준다.

3. 재귀를 작성해 대강 재귀의 흐름을 만든다.

4. 좀 더 자세한 흐름을 만든다.

5. 재귀의 끝 부분인 기저 사례 작성

완전 탐색은 간단히 만들 수 있다.

하지만 변수 Cnt를 넣어 solve함수의 호출 횟수를 확인하자

이를 이용해 시간 복잡도를 계산해보면

n = 1 : O(1)

n = 2 : O(3)

n = 3 : O(7)

n = 4 : O(15)

n = 5 : O(31)

n = 6 : O(63)

으로 2^n - 1임을 알 수 있다.

이 문제에서 n의 최대 값은 100이므로 2^100은 주어진 시간 5초로도 불가능하다..

하지만 조금만 생각해도 중복되어 계산되고 있는 데이터가 있고

최적화 문제에도 잘 어울리는 DP를 사용해본다.

완전 탐색 + 메모리제이션

1. dp table에 무엇을 저장할지 생각한다. (완전탐색의 점화식과 비슷하다)

2. 메모리제이션 사용

위와 마찬가지로 카운팅을 해보면

n = 1 : O(1)

n = 2 : O(3)

n = 3 : O(7)

n = 4 : O(13)

n = 5 : O(21)

n = 6 : O(31)

로 O(n)보다 낮게 나오는걸 확인할 수 있다.

||문제 이해

2^20 * 2^20 의 판에서 각 칸은 흰,검으로 나타낼 수 있다.

1.모든 칸이 검은 색일 경우 = b 로 나타낸다.

2.모든 칸이 하얀 색일 경우 = w 로 나타낸다.

3.모든 칸이 통일되지 않으면 판을 4등분 각 부분을 1번부터 다시 적용한다.

합치는 순서는 [좌측상단 + 우측상단 + 좌측하단 + 우측하단] 이다.

놀랍게도 이 문제는 이렇게 압축을 한 값을 입력값으로 넘겨준다.

근데 그럼 그렇지, 이 입력값을 통해 원본판의 상하반전을 적용하여 재 압축한 결과를 출력해라.

처음예시에서 이게 무슨말인지 몰라 이해하는데 시간이 걸렸다.

저게 띄어써서 헷갈리는데 xxwwwb  xwxxbbbww  xxxwwbbbwwwwb  b로 보면 이해할 수 있다.

||해결 계획

이런 하나의 페이지를 나누어 문제를 해결 = 분할정복 유형

처음에 여러 생각을 했었는데 그중 하려던게

1. 원본을 구해놓고

2. 상하 반전을 적용하고

3. 다시 재압축 하는것이다.

근데 생각해보니까 굳이 상하반전을 할 필요없이 합치는 순서를 다르게 하면 상하반전 처럼 보이지 않을까 했다.

처음에 1 + 2 + 3 + 4 순서로 합했다면, 3 + 4 + 1 + 2 로 합치면 상하반전이 된다!

1. 이 아이디어로 재귀를 전개했다.

이렇게 하면 Solve가 상하반전한 문자열을 반환해 준다.( = 믿는다)

각 4부분에서도 상하반전한 문자열을 반환 한다고 한다.( = 믿는다)

그럼 결국에는 상하반전한 문자열을 반환할것이다.

2. 그리고 Base case를 생각해본다.

base case는 문제의 최소단계 즉, 계속 4등분되면서 한칸이 될 때다.

||계획 검증

이 예시로 처음으로 재귀의 마지막이 될때까지만 써보자

x는 이 그림의 압축 문자열인 xwxwbbbww 이다.

첫번째 재귀

1 : x[0] = 'x' + Solve()

두번째 재귀

1 : x[1] = 'w'

2 : x[2] = 'x' + Solve()

세번째 재귀

1 : x[3] = 'w'

2 : x[4] = 'b'

3 : x[5] = 'b'

4 : x[6] = 'b'

재조합 : bbwb반환

두번째 재귀

1 : 'w'

2 : x + bbwb

3 : x[7] = w

4 : x[8] = w

재조합 : wwwxbbwb 반환

첫번째 재귀 (제일 상단 레벨이라 한가지 밖에 없다!)

1 : 'x' + wwwxbbwb

재조합 : xwwwxbbwb 반환

출력 : xwwwxbbwb

그럼 상하반전과 맞는지 확인하자.

이대로 압축을 해보면

xwwwxbbwb로 정답이 나온다.

하지만 위의 설계와 다른부분이 있는데 첫번째 재귀가 그렇다.

이는 main에서 따로 작성해주면 될것같다! 

||구현

#include <iostream>
#include <queue>
#include <string>
using namespace std;

queue<char> q;

//현재 레벨 트리의 각 4분면 string을 구하고 재 조합하여 반환한다!
//불변식 : 이전레벨의 x는 없다.
string Solve(int lev)
{
	//base case : 1칸일때, 두 가지 경우가 있다.
	//1)최소레벨일때의 1칸, 2)최소레벨이 되지 않았을 때의 한칸
	if (lev == 0 || q.size() == 1)
	{
		string ret(1, q.front()); q.pop();
		return ret;
	}

	//1. 각 4분면의 문자열 저장
	string temp[4];
	for (int i = 0; i < 4; ++i)
	{
		temp[i] = q.front(); q.pop();
		if (temp[i] == "x") temp[i] += Solve(lev - 1);
	}

	//2. 재 합성후 반환
	return temp[2] + temp[3] + temp[0] + temp[1];
}


int main()
{
	int n; cin >> n;
	while (n--)
	{
		//1. Input value
		queue<char> tq; q = tq;
		string ts; cin >> ts;
		for (auto & d : ts) q.push(d);

		//2. Do solve
		string ret(1, q.front()); q.pop();
		if (ret == "x") ret += Solve(20);
		cout << ret << "\n";
	}
	return 0;
}

||되돌아보기

들어온 값을 앞에서 부터 빼고 싶어서 queue를 사용해 입력값을 받았다.

그리고 불변식부분을 생각안하니까 헷갈렸는데

불변식으로 확정지으니까 편하게 작성할 수 있었다.

당황했던거는 최소 트리 레벨을 0으로 해야하는데 1로 작성을 잘못했던 것

그리고 기억할것은 상하반전이라는 부분문제를 좀 더 효율적으로 생각해본것에 있다.

다른 문제에서도 부분문제를 좀 더 효율적이게 생각해야지!

||개선 코드

입력값을 큐를 쓰지 않고 순회하는 방법을 적용해봤다.

더 가벼워진 느낌이다.

string str;

//현재 레벨 트리의 각 4분면 string을 구하고 재 조합하여 반환한다!
//불변식 : 이전레벨의 x는 없다.
string Solve(string::iterator& it, int lev)
{
	//base case : 1칸일때, 두 가지 경우가 있다.
	//1)최소레벨일때의 1칸, 2)최소레벨이 되지 않았을 때의 한칸
	if (lev == 0 || it + 1 == str.end())
	{
		return string(1, *(it++));
	}

	//1. 각 4분면의 문자열 저장
	string temp[4];
	for (int i = 0; i < 4; ++i)
	{
		temp[i] = *(it++);
		if (temp[i] == "x")
		{
			temp[i] += Solve(it, lev - 1);
		}
	}

	//2. 재 합성후 반환
	return temp[2] + temp[3] + temp[0] + temp[1];
}

||문제 이해

포켓몬 도감 리스트가 주어지고

오박사가 번호를 물어보면 포켓몬의 이름을 출력,

오박사가 포켓몬의 이름을 물어보면 번호를 출력 하라.

||해결 계획

모두 직감적으로 느끼겠지만 이건 map이다.

하나 좀 고민했던게 있는데 map의 key는 하나다.

하지만 문제는 key를 번호, 이름 두가지로 묻고있다.

좀 고민하다가 나는 다 저장하기로 했다 ㅋㅋㅋ

map<string, string> 형식으로

{"1", "피카츄"}

{"피카츄","1"}

이렇게 번호도 string화 해서 map에 두번 저장하기로 했다.

||구현

#include <bits/stdc++.h>
#include <unordered_set>
using namespace std;

unordered_map<string,string> dogam;

int main()
{
	ios::sync_with_stdio(0), cin.tie(0);

	int n, m; cin >> n >> m;
	for (int i = 1; i <= n; ++i)
	{
		string str; cin >> str;
		dogam.insert({str, to_string(i)});
		dogam.insert({to_string(i), str});
	}

	while (m--)
	{
		string str; cin >> str;
		cout << dogam.find(str)->second << '\n';
	}

	return 0;
}

||되돌아보기

다른 코드들도 보니 이런식으로 두번 저장하여 풀이하는듯 했다.

문제 읽는게 재미있었던 문제

||개선 코드

#include <bits/stdc++.h>
#include <unordered_set>
using namespace std;

unordered_map<string,string> dogam;
string dogam2[1'000'005];

int main()
{
	ios::sync_with_stdio(0), cin.tie(0);

	int n, m; cin >> n >> m;
	for (int i = 1; i <= n; ++i)
	{
		string str; cin >> str;
		dogam.insert({ str, to_string(i) });
		dogam2[i] = str;
	}

	while (m--)
	{
		string str; cin >> str;
		if(isdigit(str[0]))
			cout << dogam2[stoi(str)]<< '\n';
		else
			cout << dogam.find(str)->second << '\n';
	}

	return 0;
}

map에서 숫자를 키로 받는 부분을 string배열을 만들어 따로 저장했다.

아무래도 탐색부분에 있어서 인덱스 참조는 O(1)이니까 훨씬 빨랐다.

그리고 이번에 알게된건데 isdigit은 int형을 반환한다. 반환 값이 0, 1뿐만 아니라 4 ,6이런게 나올수도 있다는 말이다.

그래서 if (isdigit(3) == true) 는 컴파일오류는 나지 않지만 원하는 결과가 나오지 않는다.

||문제 이해

자연수 m이 주어질 때, 행렬^m 을 구하라

||해결 계획

분할 정복을 사용한다.

1. 먼저 재귀의 초기형을 짜본다.

2. 그리고 m이 짝수일 경우와 홀수일 경우가 다른데 일단 짝수로 생각해보자

행렬의 짝수 거듭제곱인 A^4를 풀어보면 이렇다.

A^4 = A * A * A * A

이 식은 행렬 A의 4거듭제곱이니 Pow(A, 4)와 같다!

곱셈은 자리를 변경해도, 어떤것부터 곱하던지 값은 항상 똑같기에 분할하기 편하게 반으로 나누어보자

A^4 = (A * A) * (A * A) = A^2 * A^2

이렇게 되면 저 하나의 A^2는 Pow(A,2)로도 가능하다!

즉, A^4 = Pow(A, 2) * Pow(A, 2) 이다.

그럼 최종의 최종은 Pow(A,4) = Pow(A, 2) * Pow(A, 2) 일 것이다.

하지만 이렇게 되면 사실 분할정복의 의미가 없다.

분할정복을 정리하면서 깨달은건데

큰 그림만 놓고보면 사실 일반 재귀와 분할정복의 재귀 호출 수는 똑같다.

하나의 뭉텅이가 재귀 한번인데 각 개수를 세보면 11개로 똑같다.

근데 이 문제에서의 분할 정복이 메리트가 있는 건

※모든 분할정복이 그렇다는 건 아님

분할했을 때 A뭉텅이, B뭉텅이가 나온다고 하면

A뭉텅이의 재귀 값으로 B뭉텅이를 재귀호출하지 않고 알 수 있어서가 아닐까 싶다.

암튼 지금까지 경험상은 그렇다.

그래서 분할정복을 사용하려면 코드는 이렇게 되어야한다.

3. 이제 짝수는 되었으니 간단한 홀수를 추가한다.

A^5 = A * A^4 인건 당연한 사실

즉, A * Pow(A, A-1)로 홀수거듭제곱을 알 수 있다.

4. Base case를 추가해주면 완성이다.

||구현

Matrix Pow(Matrix mat, int m)
{
	//base case, 최소의 부분문제이므로 m이 1일때이다.
	if (m == 1) return mat;

	//홀수일 때의 답 반환
	if (m & 0x1) return mat * Pow(mat, m - 1);

	//m이 짝수일 때의 답 반환
	Matrix half = Pow(mat, m / 2);
	return half * 2;
}

||되돌아보기

책에서는 홀수일때 다른 방법도 제시했는데

pow(A, m/2) * pow(A, m/2 + 1) 이다.

내가 작성한 짝수일때 pow(A, m/2) * pow(A, m/2)와 같은 경우다.

이것도 마찬가지로 재귀호출양이 훨씬 많다.

하지만 이 방식이 더 빠르게 답을 도출하는 방법이 있는데

바로 동적계획법(DP)이다.

근데 이말을 듣고 생각해보니까 분할하는 여러 방법이 있겠다 싶었다.

그래서 무조건 반이아닌 좀 더 효율적인 분할방법을 찾아보려고도 해야겠다!

dp는 아직 내가 자신있게 풀수있는건 아니여서 얼른 속도내서 뒷장에서 공부해야겠다 = ~ =

암튼 이번 문제를 정리하면서 분할정복이 왜 재귀와 차이가 나는지 깨달았다. 

이렇게 좀 논리적인 코드를 작성하려고 노력하다보니까 예전보다 재귀 작성하기가 쉬워졌고

앞으로도 항상 더 논리적인 코드를 짜려고 노력해야겠다.

||문제 이해

이차원 좌표 평면에서 시작된다. (x,y는 uv좌표계와 같은 방향을 가지고 있다.)

드래곤 커브는 속성을 기반으로 세대마다 길어진다.

여러 드래곤 커브가 있고 특정 세대까지 길어질 때,

1 * 1 정사각형의 꼭짓점이 드래곤 커브에 속하는 개수를 구하라.

||해결 계획

제일 먼저 든 생각은

모든 드래곤 커브의 꼭짓점을 구할 수 있는가? 였다,

그 꼭짓점들을 배열에 저장하고 싶었다.

그리고 간단한 판을 생각했다.

일단 드래곤 커브의 속성인지 뭔지는 중요하지 않고 빨간색이 드래곤 커브에 해당한 꼭짓점이라 하면

좌측 상단의 칸부터 정사각형이 될 수 있는지 검사하면 간단하다고 생각했다.

즉 부분 문제를 세가지로 나누었다.

1. 드래곤 커브 생성하기

2. 드래곤 커브에 속한 꼭짓점 저장하기

3. 판의 좌측 상단부터 정사각형 검사하기

코드를 대강 작성해보자

코드를 작성하다 보니까 굳이 100 * 100개의 꼭짓점을 검사해야싶나 했다.

그래서 드래곤 커브에 속한 꼭짓점만 검사하기로 했다.

여기서 set을 사용한 이유는 위에서 사각형 검사를 할때 중복으로 검사하지 않게 하고 싶어서 그렇다.

||계획 검증

일단 3 * 3판에 모든 드래곤 커브의 좌표가 빨간 좌표에 생겼다고 하자.

1.MakeDC( )를 하면 드래곤 커브를 생성하면서 저 빨간 점들이 저장될 것이다.

위의 예시라면 밑과 같이 저장이 될 것이다.

vector<pair<int,int>> vertices ={ {1, 1}, {1, 2}, {2, 1}, {2, 2}, {2, 3}, {3, 3} } 

2.CheckRect( )에서 vertices에 저장한 빨간 점을 모두 탐색한다.

└2.1 각 원소의 우측, 하단, 우측하단이 vertices에 저장되어있는지 확인하고 모두 있으면 카운트 한다.

(이 세가지만 확인함으로서 찾는 사각형이 중복되는걸 방어했다)

{1, 1} = {2, 1}, {1, 2}, {2, 2} = 카운트O

{1, 2} = {2, 2}, {1, 3}, {2, 3} = 카운트X

{2, 1} = {3, 1}, {2, 2}, {3, 2} = 카운트X

{2, 2} = {3, 2}, {2, 3}, {3, 3} = 카운트X

{2, 3} = {3, 3}, {2, 4}, {3, 4} = 카운트X

{3, 3} = {4, 3}, {3, 4}, {4, 4} = 카운트X

최종 1개로 답이 도출된다.

흠.. 일단 검증 같은걸 해보긴 했는데 이걸 검증이라고 할 수 있는지? 모르겠다

||구현

#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> pii;
set<pii> vertices;

pii operator+(const pii & p1, const pii & p2)
{
	return { p1.first + p2.first, p1.second + p2.second };
}
pii operator-(const pii & p1, const pii & p2)
{
	return { p1.first - p2.first, p1.second - p2.second };
}
pii Rotate(pii & p)
{
	int temp = (p.second * -1);
	p.second = p.first;
	p.first = temp;
	return p;
}

//[0] : 시작 x좌표
//[1] : 시작 y좌표
//[2] : 시작 방향
//[3] : 세대
vector<vector<int>> dcProp;
vector<pii> tdc;

pii moving[4] = { {1, 0},{0, -1},{-1, 0}, {0, 1} };
void MakeDC()
{
	//1. 드래곤 커브를 개수만큼 생성한다.
	for (const auto & d : dcProp)
	{
		//1.1 0세대의 시작 좌표 저장
		pii s = { d[0], d[1] };
		tdc.push_back(s);
		//1.2 0세대의 끝점 계산, 좌표 기록
		tdc.push_back(s + moving[d[2]]);

		//1.3 세대가 성장하는가?
		if (0 < d[3])
		{
			//1.3.1	2세대이상부터, 입력 세대 만큼 커브 성장
			for (int i = 1; i <= d[3]; ++i)
			{
				pii e = tdc.back();
				int tempSize = tdc.size();
				//이전까지의 꼭짓점 회전 시켜 좌표 기록
				for (int j = tempSize - 2; 0 <= j ; --j)
				{
					pii t = tdc[j] - e;
					tdc.push_back(e + Rotate(t));
				}
			}
		}

		//최종 저장
		for (const auto & d : tdc)
		{
			vertices.insert(d);
		}
		tdc.resize(0);
	}
}

// (x, y) 형태의 좌표
pii preset[3] = { {1, 0}, {0, 1}, {1, 1} };
int ret = 0;
void CheckRect()
{
	//1. 각 꼭짓점 검사
	for (auto & d : vertices)
	{
		bool isRect = true;
		for (int i = 0; i < 3 && isRect; ++i)
		{
			if (vertices.find(d + preset[i]) == vertices.end()) isRect = false;
		}

		if (isRect == true) ++ret;
	}
}

int main()
{
	ios::sync_with_stdio(0), cin.tie(0);

	int c; cin >> c;
	dcProp.resize(c);
	for (int i = 0; i < c; ++i)
	{
		dcProp[i].resize(4);
		cin >> dcProp[i][0] >> dcProp[i][1] >> dcProp[i][2] >> dcProp[i][3];
	}
	MakeDC();
	CheckRect();

	cout << ret;
	return 0;
}

||되돌아보기

막힌 부분이 두 부분이 있었다.

1.문제의 조건을 잘못 이해

문제를 풀면서 점점 내가 문제를 이해 완벽히 이해하지 못한다고 생각이 들었다.

코드는 완성했는데 예시의 답과는 다르게 나오고,

조건이 틀렸는지 확인하고, 틀린 조건 수정하고 => 이 단계 반복이 좀 많았다;

문제 조금보고 이해했다고 깝치지말고 

다음에는 내가 이해한 것과 예시가 같은지도 제대로 비교해서 문제를 확실히 이해하고 넘어가야겠다😪

2.다양한 예시

내가 0세대에서 1세대로 넘어가는 예시만 생각하는 바람에

끝 좌표 이전의 모든 좌표를 회전시켜서 저장하지 못하고 시작 좌표만 회전시켜서 저장되었다.

너무 많은 예시는 아니더라도 최소 2개정도의 예시를 생각하자

||개선 코드

내 코드에서 일단 가볍게 개선 해봤다.

일단 회전 부분을 (y * -1, x)으로 간단히 했고

#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;

//[0] : start X //[1] : start Y //[2] : 시작 방향 //[3] : 세대
vector<vector<int>> dcProp;
set<pii> vertices;
vector<pii> tdc;

pii operator+(const pii & p1, const pii & p2)
{
	return { p1.first + p2.first, p1.second + p2.second };
}
pii operator-(const pii & p1, const pii & p2)
{
	return { p1.first - p2.first, p1.second - p2.second };
}

pii moveSet[4] = { {1, 0},{0, -1},{-1, 0}, {0, 1} };
void MakeDC()
{
	//1. 드래곤 커브를 개수만큼 생성한다.
	for (const auto & d : dcProp)
	{
		//1.1 0세대의 시작, 끝 좌표 저장
		pii s = { d[0], d[1] };
		tdc.push_back(s);
		tdc.push_back(s + moveSet[d[2]]);

		//1.2 1세대이상부터, 입력 세대 만큼 커브 성장
		for (int i = 1; i <= d[3]; ++i)
		{
			pii e = tdc.back();
			int tempSize = tdc.size();

			//1.2.1 끝점 이전의 꼭짓점들 회전 시켜 좌표 기록
			for (int j = tempSize - 2; 0 <= j ; --j)
			{
				pii t = tdc[j] - e;
				tdc.push_back(e + make_pair(t.second * -1, t.first));
			}
		}

		//최종 저장
		for (const auto & d : tdc)
		{
			vertices.insert(d);
		}
		tdc.resize(0);
	}
}

pii checkSet[3] = { {1, 0}, {0, 1}, {1, 1} };
int CheckRect()
{
	int ret = 0;
	//저장한 각 꼭짓점 검사
	for (auto & d : vertices)
	{
		bool isRect = true;
		for (int i = 0; i < 3 && isRect; ++i)
		{
			if (vertices.find(d + checkSet[i]) == vertices.end()) isRect = false;
		}
		if (isRect == true) ++ret;
	}
	return ret;
}

int main()
{
	ios::sync_with_stdio(0), cin.tie(0);

	//1. Input values
	int c; cin >> c;
	dcProp.resize(c);
	for (int i = 0; i < c; ++i)
	{
		dcProp[i].resize(4);
		cin >> dcProp[i][0] >> dcProp[i][1] >> dcProp[i][2] >> dcProp[i][3];
	}

	//2. Do calculate & Print result
	MakeDC();
	cout << CheckRect();
	return 0;
}

||문제 이해

N * N형 배열에 모든 원소는 -1, 0, 1 중 하나의 값을 가진다.

1) 모든 배열의 원소 값이 같으면 그 값에 해당하는 카운트를 한다.

2) 모든 배열의 원소 값이 다르면 배열을 9등분하여 다시 1번으로 돌아간다.

이 규칙을 적용했을 때 각 -1, 0, 1이 가지는 카운트 값을 출력하여라

||해결 계획

예전에 이런 종류의 문제를 보아서

보자마자 분할 정복이 떠올랐다.

그리고 기본형으로 이러한 함수를 생각했다.

이 재귀의 능력은

1. Recursive가 종이의 해당 범위를 탐색하여 모든 원소가 같은지 참, 거짓을 나눈다.

2. 참이면 카운팅을 할 수 있다.

일단 할 수 있다고 믿자.(이 재귀를 믿어보자)

그럼 이제 9등분을 하고 각 나눈 구역마다 이 Recursive를 돌려주자.

여기서 마무리하면 재귀가 무한 반복 될수도 있기에 base case를 넣어주자

base case는 이 문제의 최소 단계로, 1 x 1칸일때라고 볼 수 있다.

1 * 1칸일 때는 모든 칸이 같으므로 카운팅도 해준다.

||계획 검증

간단히 3 * 3 칸 짜리로 생각해보자

0, 0, 0

1, 1, 1

0, 0, 0

첫 재귀는 false로 9칸으로 나눌것이다.

1칸, 2칸, 3칸,...,9칸 각 칸마다 재귀를 실행한다.

1칸 재귀 - 1칸이므로 카운팅 후 return

2칸 재귀 - 1칸이므로 카운팅 후 return

...

9칸 재귀 - 1칸이므로 카운팅 후 return

그럼 모두 카운팅을 하고 돌아와 답이 나온다.

이는 

0, 0, 0

0, 0, 0

0, 0, 0

처럼 모든 칸이 같은 경우에도 답이 나온다.

그럼 마지막으로 9 * 9칸 짜리로 생각해보자

0,0,0, 1,1,1, 0,0,0

0,0,0, 1,1,1, 0,0,0

0,0,0, 1,1,1, 0,0,0

1,1,1, 0,0,0, 1,1,1

1,1,1, 0,0,0, 1,1,1

1,1,1, 0,0,0, 1,1,1

0,0,0, 1,1,1, 0,0,0

0,0,0, 1,1,1, 0,0,0

0,0,0, 1,1,1, 0,0,1

첫 재귀는 false로 3*3짜리로 9칸을 나눌것이다.

1칸, 2칸, 3칸,...,9칸 각 칸마다 재귀를 실행한다

1칸 재귀 - 3* 3칸이므로 될것이다. 왜냐하면 위에서 됐으니까

2칸 재귀 - 3* 3칸이므로 될것이다. 왜냐하면 위에서 됐으니까

...

9칸 재귀 - false지만 될것이다. 왜냐하면 위에서 됐으니까

||구현

int n;
vector<vector<int>> maps;
int ret[3];

//N이 9라면 S는 0, E는 8이 들어온다.
void Counting(int yS, int yE, int xS, int xE)
{
	//모든 타일이 같은지 확인 (자동으로 한칸일때도 적용된다.
	bool isAllSame = true;
	int std = maps[yS][xS];

	for (int y = yS; y <= yE; ++y)
	{
		for (int x = xS; x <= xE; ++x)
		{
			if (maps[y][x] != std)
			{
				isAllSame = false;
				break;
			}
		}
		if (isAllSame == false) break;
	}
	
	//모두 같으면 카운팅, 종료
	if (isAllSame == true)
	{
		ret[maps[yS][xS] + 1] += 1;
		return;
	}
	
	//9등분한 배열마다 재귀를 들어간다.
	for (int y = 0; y < 3; ++y)
	{
		int divStd_y = (yE - yS) / 3 + 1;
		int tempS_y = yS + (divStd_y * y);

		for (int x = 0; x < 3; ++x)
		{
			int divStd_x = (xE - xS) / 3 + 1;
			int tempS_x = xS + (divStd_x * x);
			Counting(tempS_y, tempS_y + divStd_y - 1, tempS_x, tempS_x + divStd_x - 1);
		}
	}
	return;
}

int main()
{
	//1. Input values
	ios::sync_with_stdio(0), cin.tie(0);
	cin >> n;

	maps.resize(n + 1);
	for (int y = 0; y < n; ++y)
	{
		maps[y].resize(n + 1);
		for (int x = 0; x < n; ++x)
		{
			int temp; cin >> temp;
			maps[y][x] = temp;
		}
	}
	
	//2. Do Recursive
	Counting(0, n - 1, 0, n - 1);

	//3. Print
	for (const auto & d : ret)
	{
		cout << d << "\n";
	}
	return 0;
}

||되돌아보기

설계의 뒷심이 부족해서 자꾸 코드 추가하고, 추가하면서 매개변수도 들어가고, 매개변수 들어간거 다 수정하고...

설계가 잘 했다고 생각했지만 코드를 작성하고 나니까 헛점이 많이 보였다ㅜ

보면 검증할때의 코드도 길이를 매개변수로 받았다면 더 빨리 깔끔하게 풀수 있을것 같아서 아쉽다.

그리고 처음 제출할 때 오답이 자꾸 나왔는데

자료형 문제로 틀려버렸다 =~=

이런 실수는 다시 하지 말도록 하자ㅠ

||개선 코드

흠.. 평균 속도로 풀이하긴 했는데 빠르게 푼 코드를 보면 시간이 많이 차이나서

한번 개선을 좀 해봤다.

먼저 이번에 알게 된건데 이중 반복문으로 탐색중에

bool형 변수의 값이 바뀌면 이중 반복문을 탈출해야할때 이런 방법도 있는걸 배웠다.

사실 속도야 비슷하겠지만 for문 조건부에 검사를 하여 우측이 좀더 깔끔해보인다.

그리고 9등분을 하는 과정이 좀 힘들게 하는 느낌이여서

좀 더 간단하게 개선해봤다.

void Counting(int yS, int xS, int l)
{
	//모든 타일이 같은지 확인 (자동으로 한칸일때도 적용된다.
	bool isAllSame = true;
	for (int y = yS; (y < yS + l) && isAllSame; ++y)
	{
		for (int x = xS; (x < xS + l) && isAllSame; ++x)
		{
			if (maps[y][x] != maps[yS][xS])
			{
				isAllSame = false;
			}
		}
	}

	//모두 같다면 카운트
	if (isAllSame == true)
	{
		++ret[maps[yS][xS] + 1];
		return;
	}
	
	//9등분한 배열마다 재귀를 들어간다.
	l /= 3;
	for (int y = 0; y < 3; ++y)
	{
		for (int x = 0; x < 3; ++x)
		{
			Counting(yS + l * y, xS + l * x, l);
		}
	}
	return;
}

속도는 더이상 크게 변하지는 않았지만 그래도 코드를 많이 가볍게 개선해서 기분은 좋다!

||문제 이해

N이 주어질 때 1 ~ N까지의 합을 분할 정복으로 구하라

||해결 계획

분할 정복

||계획 검증

문제는 1 + 2 + 3 + ... + n이다.

먼저 단순 재귀형태의 풀이 함수는 이렇다.

이 문제를 최소한의 부분 문제로 분할하고 반으로 분할한다. (일단 짝수로 예시를 들면서 보자)

※오타 : 글에 써진 "2/n" 은 "n/2" 다.

1 ~ n/2 의 앞부분, n/2 + 1 ~ n 까지의 뒷부분

이 앞부분은 앞의 fastSum으로 해결할수있다. fastSum(n / 2)

하지만 fastSum은 무조건 1부터 n까지의 합이기 때문에 뒷부분에서는 사용할 수 없다.

그럼 뒷부분도 fastSum으로 해결하게끔 바꾸어 보자.

뒷부분만 가져와 바꾸어 본다.

※오타 : 여기도 마찬가지로 글에 써진 "2/n" 은 "n/2" 다.

이렇게 뒷부분도 fastSum을 이용하여 풀수 있게 되었다.

그럼 다시 앞으로 돌아가서 앞부분과 뒷부분을 합해서 정리하면 이렇다.

일단 짝수만 fastSum을 이용하여 풀수 있다.

그럼 홀수는 어떻게 하면 될까?

간단히 생각하면 바로 알수 있다.

fastSum에 짝수 n을 넣으면 1 ~ n까지의 합이 나온다!

그럼 n이 홀수라면 n - 1은 짝수다.

이를 더해보면 n + fastSum(n - 1) 로 계산이 가능하다.

시간복잡도는 분할정복이니 O(n log n)이 나오겠다.

재귀 한번에 O(log n)이 나오니까

여러번의 재귀 호출은 당연히 O(n log n)이다.

||구현

int fastSum(int n)
{
	//Base case
	if (n == 1) return 1;
	//홀수일때
	if (n & 0x1) return n + fastSum(n - 1);
	//짝수일때
	return fastSum(n / 2) * 2 + ((n * n) / 4);
}

||되돌아보기

하나하나 정리해보면서 이해하니까

분할 정복에 대해 좀 많이 다가간거 같다.

다음에도 이렇게 논리적으로 재귀를 설계하는 시도를 해야겠다.