||문제 이해
2^20 * 2^20 의 판에서 각 칸은 흰,검으로 나타낼 수 있다.
1.모든 칸이 검은 색일 경우 = b 로 나타낸다.
2.모든 칸이 하얀 색일 경우 = w 로 나타낸다.
3.모든 칸이 통일되지 않으면 판을 4등분 각 부분을 1번부터 다시 적용한다.
합치는 순서는 [좌측상단 + 우측상단 + 좌측하단 + 우측하단] 이다.
놀랍게도 이 문제는 이렇게 압축을 한 값을 입력값으로 넘겨준다.
근데 그럼 그렇지, 이 입력값을 통해 원본판의 상하반전을 적용하여 재 압축한 결과를 출력해라.
처음예시에서 이게 무슨말인지 몰라 이해하는데 시간이 걸렸다.

저게 띄어써서 헷갈리는데 xxwwwb xwxxbbbww xxxwwbbbwwwwb b로 보면 이해할 수 있다.
||해결 계획
이런 하나의 페이지를 나누어 문제를 해결 = 분할정복 유형
처음에 여러 생각을 했었는데 그중 하려던게
1. 원본을 구해놓고
2. 상하 반전을 적용하고
3. 다시 재압축 하는것이다.
근데 생각해보니까 굳이 상하반전을 할 필요없이 합치는 순서를 다르게 하면 상하반전 처럼 보이지 않을까 했다.
처음에 1 + 2 + 3 + 4 순서로 합했다면, 3 + 4 + 1 + 2 로 합치면 상하반전이 된다!
1. 이 아이디어로 재귀를 전개했다.
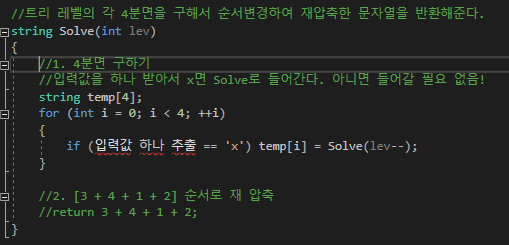
이렇게 하면 Solve가 상하반전한 문자열을 반환해 준다.( = 믿는다)
각 4부분에서도 상하반전한 문자열을 반환 한다고 한다.( = 믿는다)
그럼 결국에는 상하반전한 문자열을 반환할것이다.
2. 그리고 Base case를 생각해본다.

base case는 문제의 최소단계 즉, 계속 4등분되면서 한칸이 될 때다.
||계획 검증
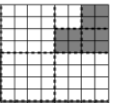
이 예시로 처음으로 재귀의 마지막이 될때까지만 써보자
x는 이 그림의 압축 문자열인 xwxwbbbww 이다.
첫번째 재귀
1 : x[0] = 'x' + Solve()
두번째 재귀
1 : x[1] = 'w'
2 : x[2] = 'x' + Solve()
세번째 재귀
1 : x[3] = 'w'
2 : x[4] = 'b'
3 : x[5] = 'b'
4 : x[6] = 'b'
재조합 : bbwb반환
두번째 재귀
1 : 'w'
2 : x + bbwb
3 : x[7] = w
4 : x[8] = w
재조합 : wwwxbbwb 반환
첫번째 재귀 (제일 상단 레벨이라 한가지 밖에 없다!)
1 : 'x' + wwwxbbwb
재조합 : xwwwxbbwb 반환
출력 : xwwwxbbwb
그럼 상하반전과 맞는지 확인하자.

이대로 압축을 해보면
xwwwxbbwb로 정답이 나온다.
하지만 위의 설계와 다른부분이 있는데 첫번째 재귀가 그렇다.
이는 main에서 따로 작성해주면 될것같다!
||구현
#include <iostream>
#include <queue>
#include <string>
using namespace std;
queue<char> q;
//현재 레벨 트리의 각 4분면 string을 구하고 재 조합하여 반환한다!
//불변식 : 이전레벨의 x는 없다.
string Solve(int lev)
{
//base case : 1칸일때, 두 가지 경우가 있다.
//1)최소레벨일때의 1칸, 2)최소레벨이 되지 않았을 때의 한칸
if (lev == 0 || q.size() == 1)
{
string ret(1, q.front()); q.pop();
return ret;
}
//1. 각 4분면의 문자열 저장
string temp[4];
for (int i = 0; i < 4; ++i)
{
temp[i] = q.front(); q.pop();
if (temp[i] == "x") temp[i] += Solve(lev - 1);
}
//2. 재 합성후 반환
return temp[2] + temp[3] + temp[0] + temp[1];
}
int main()
{
int n; cin >> n;
while (n--)
{
//1. Input value
queue<char> tq; q = tq;
string ts; cin >> ts;
for (auto & d : ts) q.push(d);
//2. Do solve
string ret(1, q.front()); q.pop();
if (ret == "x") ret += Solve(20);
cout << ret << "\n";
}
return 0;
}
||되돌아보기
들어온 값을 앞에서 부터 빼고 싶어서 queue를 사용해 입력값을 받았다.
그리고 불변식부분을 생각안하니까 헷갈렸는데
불변식으로 확정지으니까 편하게 작성할 수 있었다.
당황했던거는 최소 트리 레벨을 0으로 해야하는데 1로 작성을 잘못했던 것
그리고 기억할것은 상하반전이라는 부분문제를 좀 더 효율적으로 생각해본것에 있다.
다른 문제에서도 부분문제를 좀 더 효율적이게 생각해야지!
||개선 코드
입력값을 큐를 쓰지 않고 순회하는 방법을 적용해봤다.
더 가벼워진 느낌이다.
string str;
//현재 레벨 트리의 각 4분면 string을 구하고 재 조합하여 반환한다!
//불변식 : 이전레벨의 x는 없다.
string Solve(string::iterator& it, int lev)
{
//base case : 1칸일때, 두 가지 경우가 있다.
//1)최소레벨일때의 1칸, 2)최소레벨이 되지 않았을 때의 한칸
if (lev == 0 || it + 1 == str.end())
{
return string(1, *(it++));
}
//1. 각 4분면의 문자열 저장
string temp[4];
for (int i = 0; i < 4; ++i)
{
temp[i] = *(it++);
if (temp[i] == "x")
{
temp[i] += Solve(it, lev - 1);
}
}
//2. 재 합성후 반환
return temp[2] + temp[3] + temp[0] + temp[1];
}
algospot.com :: QUADTREE
쿼드 트리 뒤집기 문제 정보 문제 대량의 좌표 데이터를 메모리 안에 압축해 저장하기 위해 사용하는 여러 기법 중 쿼드 트리(quad tree)란 것이 있습니다. 주어진 공간을 항상 4개로 분할해 재귀적
algospot.com

'코딩 테스트 > 알고리즘 풀이' 카테고리의 다른 글
| [LV3] 연습 문제 (0) | 2025.04.14 |
|---|---|
| [LV1] 복습 문제 (0) | 2025.04.13 |
| [LV1] 연습 문제 (0) | 2025.04.12 |
| [알고스팟 - TRIANGLEPATH] 삼각형 위의 최대 경로 (0) | 2023.01.08 |
| [백준 - 1620] 나는야 포켓몬 마스터 이다솜 (0) | 2022.12.09 |
| [종만북] 행렬의 거듭제곱 (0) | 2022.12.07 |
| [백준 - 15685] 드래곤 커브 (0) | 2022.12.06 |
| [종만북] 수열의 빠른 합 (0) | 2022.12.06 |

