||문제 이해
N * N형 배열에 모든 원소는 -1, 0, 1 중 하나의 값을 가진다.
1) 모든 배열의 원소 값이 같으면 그 값에 해당하는 카운트를 한다.
2) 모든 배열의 원소 값이 다르면 배열을 9등분하여 다시 1번으로 돌아간다.
이 규칙을 적용했을 때 각 -1, 0, 1이 가지는 카운트 값을 출력하여라
||해결 계획
예전에 이런 종류의 문제를 보아서
보자마자 분할 정복이 떠올랐다.
그리고 기본형으로 이러한 함수를 생각했다.

이 재귀의 능력은
1. Recursive가 종이의 해당 범위를 탐색하여 모든 원소가 같은지 참, 거짓을 나눈다.
2. 참이면 카운팅을 할 수 있다.
일단 할 수 있다고 믿자.(이 재귀를 믿어보자)
그럼 이제 9등분을 하고 각 나눈 구역마다 이 Recursive를 돌려주자.

여기서 마무리하면 재귀가 무한 반복 될수도 있기에 base case를 넣어주자
base case는 이 문제의 최소 단계로, 1 x 1칸일때라고 볼 수 있다.

1 * 1칸일 때는 모든 칸이 같으므로 카운팅도 해준다.
||계획 검증
간단히 3 * 3 칸 짜리로 생각해보자
0, 0, 0
1, 1, 1
0, 0, 0
첫 재귀는 false로 9칸으로 나눌것이다.
1칸, 2칸, 3칸,...,9칸 각 칸마다 재귀를 실행한다.
1칸 재귀 - 1칸이므로 카운팅 후 return
2칸 재귀 - 1칸이므로 카운팅 후 return
...
9칸 재귀 - 1칸이므로 카운팅 후 return
그럼 모두 카운팅을 하고 돌아와 답이 나온다.
이는
0, 0, 0
0, 0, 0
0, 0, 0
처럼 모든 칸이 같은 경우에도 답이 나온다.
그럼 마지막으로 9 * 9칸 짜리로 생각해보자
0,0,0, 1,1,1, 0,0,0
0,0,0, 1,1,1, 0,0,0
0,0,0, 1,1,1, 0,0,0
1,1,1, 0,0,0, 1,1,1
1,1,1, 0,0,0, 1,1,1
1,1,1, 0,0,0, 1,1,1
0,0,0, 1,1,1, 0,0,0
0,0,0, 1,1,1, 0,0,0
0,0,0, 1,1,1, 0,0,1
첫 재귀는 false로 3*3짜리로 9칸을 나눌것이다.
1칸, 2칸, 3칸,...,9칸 각 칸마다 재귀를 실행한다
1칸 재귀 - 3* 3칸이므로 될것이다. 왜냐하면 위에서 됐으니까
2칸 재귀 - 3* 3칸이므로 될것이다. 왜냐하면 위에서 됐으니까
...
9칸 재귀 - false지만 될것이다. 왜냐하면 위에서 됐으니까
||구현
int n;
vector<vector<int>> maps;
int ret[3];
//N이 9라면 S는 0, E는 8이 들어온다.
void Counting(int yS, int yE, int xS, int xE)
{
//모든 타일이 같은지 확인 (자동으로 한칸일때도 적용된다.
bool isAllSame = true;
int std = maps[yS][xS];
for (int y = yS; y <= yE; ++y)
{
for (int x = xS; x <= xE; ++x)
{
if (maps[y][x] != std)
{
isAllSame = false;
break;
}
}
if (isAllSame == false) break;
}
//모두 같으면 카운팅, 종료
if (isAllSame == true)
{
ret[maps[yS][xS] + 1] += 1;
return;
}
//9등분한 배열마다 재귀를 들어간다.
for (int y = 0; y < 3; ++y)
{
int divStd_y = (yE - yS) / 3 + 1;
int tempS_y = yS + (divStd_y * y);
for (int x = 0; x < 3; ++x)
{
int divStd_x = (xE - xS) / 3 + 1;
int tempS_x = xS + (divStd_x * x);
Counting(tempS_y, tempS_y + divStd_y - 1, tempS_x, tempS_x + divStd_x - 1);
}
}
return;
}
int main()
{
//1. Input values
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
maps.resize(n + 1);
for (int y = 0; y < n; ++y)
{
maps[y].resize(n + 1);
for (int x = 0; x < n; ++x)
{
int temp; cin >> temp;
maps[y][x] = temp;
}
}
//2. Do Recursive
Counting(0, n - 1, 0, n - 1);
//3. Print
for (const auto & d : ret)
{
cout << d << "\n";
}
return 0;
}||되돌아보기
설계의 뒷심이 부족해서 자꾸 코드 추가하고, 추가하면서 매개변수도 들어가고, 매개변수 들어간거 다 수정하고...
설계가 잘 했다고 생각했지만 코드를 작성하고 나니까 헛점이 많이 보였다ㅜ
보면 검증할때의 코드도 길이를 매개변수로 받았다면 더 빨리 깔끔하게 풀수 있을것 같아서 아쉽다.
그리고 처음 제출할 때 오답이 자꾸 나왔는데
자료형 문제로 틀려버렸다 =~=
이런 실수는 다시 하지 말도록 하자ㅠ
||개선 코드
흠.. 평균 속도로 풀이하긴 했는데 빠르게 푼 코드를 보면 시간이 많이 차이나서
한번 개선을 좀 해봤다.
먼저 이번에 알게 된건데 이중 반복문으로 탐색중에
bool형 변수의 값이 바뀌면 이중 반복문을 탈출해야할때 이런 방법도 있는걸 배웠다.

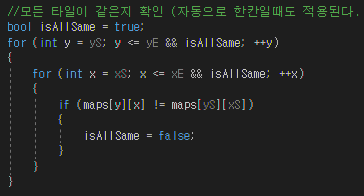
사실 속도야 비슷하겠지만 for문 조건부에 검사를 하여 우측이 좀더 깔끔해보인다.
그리고 9등분을 하는 과정이 좀 힘들게 하는 느낌이여서
좀 더 간단하게 개선해봤다.
void Counting(int yS, int xS, int l)
{
//모든 타일이 같은지 확인 (자동으로 한칸일때도 적용된다.
bool isAllSame = true;
for (int y = yS; (y < yS + l) && isAllSame; ++y)
{
for (int x = xS; (x < xS + l) && isAllSame; ++x)
{
if (maps[y][x] != maps[yS][xS])
{
isAllSame = false;
}
}
}
//모두 같다면 카운트
if (isAllSame == true)
{
++ret[maps[yS][xS] + 1];
return;
}
//9등분한 배열마다 재귀를 들어간다.
l /= 3;
for (int y = 0; y < 3; ++y)
{
for (int x = 0; x < 3; ++x)
{
Counting(yS + l * y, xS + l * x, l);
}
}
return;
}
속도는 더이상 크게 변하지는 않았지만 그래도 코드를 많이 가볍게 개선해서 기분은 좋다!


