||문제 이해
6
1 2
3 7 4
9 4 1 7
2 7 5 9 4과 같은 형태의 삼각형이 주어지며 맨 위에서 한번에 한칸씩 내려갈 수 있다.
내려가는 방향은 바로 아래와 그 한칸 오른쪽으로 내려갈 수 있으며
모든 경로중 최대값을 구하라.
||해결 계획
이번 포스팅은
문제를 보면서 "이렇게 생각을 전개해 나가면 좋겠다라고" 정리한 걸 중심으로 작성하겠다.
완전탐색
1. 답이 최대 합을 출력하라니까 일단 최대 합을 반환하는 함수형태를 만든다.

2. 좀 더 디테일하게 추가 해준다.

3. 재귀를 작성해 대강 재귀의 흐름을 만든다.

4. 좀 더 자세한 흐름을 만든다.
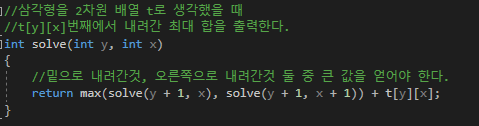
5. 재귀의 끝 부분인 기저 사례 작성

완전 탐색은 간단히 만들 수 있다.
하지만 변수 Cnt를 넣어 solve함수의 호출 횟수를 확인하자


이를 이용해 시간 복잡도를 계산해보면
n = 1 : O(1)
n = 2 : O(3)
n = 3 : O(7)
n = 4 : O(15)
n = 5 : O(31)
n = 6 : O(63)
으로 2^n - 1임을 알 수 있다.
이 문제에서 n의 최대 값은 100이므로 2^100은 주어진 시간 5초로도 불가능하다..
하지만 조금만 생각해도 중복되어 계산되고 있는 데이터가 있고
최적화 문제에도 잘 어울리는 DP를 사용해본다.
완전 탐색 + 메모리제이션
1. dp table에 무엇을 저장할지 생각한다. (완전탐색의 점화식과 비슷하다)

2. 메모리제이션 사용

위와 마찬가지로 카운팅을 해보면
n = 1 : O(1)
n = 2 : O(3)
n = 3 : O(7)
n = 4 : O(13)
n = 5 : O(21)
n = 6 : O(31)
로 O(n)보다 낮게 나오는걸 확인할 수 있다.
'코딩 테스트 > 알고리즘 풀이' 카테고리의 다른 글
| [LV3] 복습 문제 (2) | 2025.04.15 |
|---|---|
| [LV3] 연습 문제 (0) | 2025.04.14 |
| [LV1] 복습 문제 (0) | 2025.04.13 |
| [LV1] 연습 문제 (0) | 2025.04.12 |
| [알고스팟 - QUADTREE] 쿼드 트리 뒤집기 (0) | 2022.12.10 |
| [백준 - 1620] 나는야 포켓몬 마스터 이다솜 (0) | 2022.12.09 |
| [종만북] 행렬의 거듭제곱 (0) | 2022.12.07 |
| [백준 - 15685] 드래곤 커브 (0) | 2022.12.06 |

