||문제 이해
N이 주어질 때 1 ~ N까지의 합을 분할 정복으로 구하라
||해결 계획
분할 정복
||계획 검증
문제는 1 + 2 + 3 + ... + n이다.
먼저 단순 재귀형태의 풀이 함수는 이렇다.
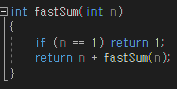
이 문제를 최소한의 부분 문제로 분할하고 반으로 분할한다. (일단 짝수로 예시를 들면서 보자)

※오타 : 글에 써진 "2/n" 은 "n/2" 다.
1 ~ n/2 의 앞부분, n/2 + 1 ~ n 까지의 뒷부분
이 앞부분은 앞의 fastSum으로 해결할수있다. fastSum(n / 2)
하지만 fastSum은 무조건 1부터 n까지의 합이기 때문에 뒷부분에서는 사용할 수 없다.
그럼 뒷부분도 fastSum으로 해결하게끔 바꾸어 보자.
뒷부분만 가져와 바꾸어 본다.

※오타 : 여기도 마찬가지로 글에 써진 "2/n" 은 "n/2" 다.
이렇게 뒷부분도 fastSum을 이용하여 풀수 있게 되었다.
그럼 다시 앞으로 돌아가서 앞부분과 뒷부분을 합해서 정리하면 이렇다.

일단 짝수만 fastSum을 이용하여 풀수 있다.
그럼 홀수는 어떻게 하면 될까?
간단히 생각하면 바로 알수 있다.
fastSum에 짝수 n을 넣으면 1 ~ n까지의 합이 나온다!
그럼 n이 홀수라면 n - 1은 짝수다.
이를 더해보면 n + fastSum(n - 1) 로 계산이 가능하다.
시간복잡도는 분할정복이니 O(n log n)이 나오겠다.
재귀 한번에 O(log n)이 나오니까
여러번의 재귀 호출은 당연히 O(n log n)이다.
||구현
int fastSum(int n)
{
//Base case
if (n == 1) return 1;
//홀수일때
if (n & 0x1) return n + fastSum(n - 1);
//짝수일때
return fastSum(n / 2) * 2 + ((n * n) / 4);
}||되돌아보기
하나하나 정리해보면서 이해하니까
분할 정복에 대해 좀 많이 다가간거 같다.
다음에도 이렇게 논리적으로 재귀를 설계하는 시도를 해야겠다.
'코딩 테스트 > 알고리즘 풀이' 카테고리의 다른 글
| [알고스팟 - QUADTREE] 쿼드 트리 뒤집기 (0) | 2022.12.10 |
|---|---|
| [백준 - 1620] 나는야 포켓몬 마스터 이다솜 (0) | 2022.12.09 |
| [종만북] 행렬의 거듭제곱 (0) | 2022.12.07 |
| [백준 - 15685] 드래곤 커브 (0) | 2022.12.06 |
| [알고스팟 - TSP1] Traveling Salesman Problem 1 (0) | 2022.12.04 |
| [백준 - 1560] 비숍 (0) | 2022.12.03 |
| [알고스팟 - PICNIC] 소풍 (0) | 2022.12.02 |
| [프로그래머스] 신규 아이디 추천 (0) | 2022.09.16 |

