||문제 이해
이차원 좌표 평면에서 시작된다. (x,y는 uv좌표계와 같은 방향을 가지고 있다.)
드래곤 커브는 속성을 기반으로 세대마다 길어진다.
여러 드래곤 커브가 있고 특정 세대까지 길어질 때,
1 * 1 정사각형의 꼭짓점이 드래곤 커브에 속하는 개수를 구하라.
||해결 계획
제일 먼저 든 생각은
모든 드래곤 커브의 꼭짓점을 구할 수 있는가? 였다,
그 꼭짓점들을 배열에 저장하고 싶었다.
그리고 간단한 판을 생각했다.

일단 드래곤 커브의 속성인지 뭔지는 중요하지 않고 빨간색이 드래곤 커브에 해당한 꼭짓점이라 하면
좌측 상단의 칸부터 정사각형이 될 수 있는지 검사하면 간단하다고 생각했다.
즉 부분 문제를 세가지로 나누었다.
1. 드래곤 커브 생성하기
2. 드래곤 커브에 속한 꼭짓점 저장하기
3. 판의 좌측 상단부터 정사각형 검사하기
코드를 대강 작성해보자
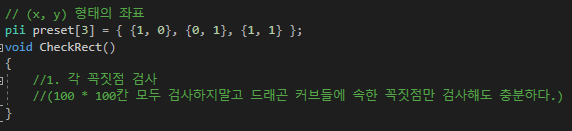
코드를 작성하다 보니까 굳이 100 * 100개의 꼭짓점을 검사해야싶나 했다.
그래서 드래곤 커브에 속한 꼭짓점만 검사하기로 했다.
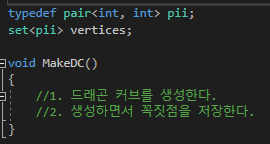
여기서 set을 사용한 이유는 위에서 사각형 검사를 할때 중복으로 검사하지 않게 하고 싶어서 그렇다.
||계획 검증
일단 3 * 3판에 모든 드래곤 커브의 좌표가 빨간 좌표에 생겼다고 하자.

1.MakeDC( )를 하면 드래곤 커브를 생성하면서 저 빨간 점들이 저장될 것이다.
위의 예시라면 밑과 같이 저장이 될 것이다.
vector<pair<int,int>> vertices ={ {1, 1}, {1, 2}, {2, 1}, {2, 2}, {2, 3}, {3, 3} }
2.CheckRect( )에서 vertices에 저장한 빨간 점을 모두 탐색한다.
└2.1 각 원소의 우측, 하단, 우측하단이 vertices에 저장되어있는지 확인하고 모두 있으면 카운트 한다.
(이 세가지만 확인함으로서 찾는 사각형이 중복되는걸 방어했다)
{1, 1} = {2, 1}, {1, 2}, {2, 2} = 카운트O
{1, 2} = {2, 2}, {1, 3}, {2, 3} = 카운트X
{2, 1} = {3, 1}, {2, 2}, {3, 2} = 카운트X
{2, 2} = {3, 2}, {2, 3}, {3, 3} = 카운트X
{2, 3} = {3, 3}, {2, 4}, {3, 4} = 카운트X
{3, 3} = {4, 3}, {3, 4}, {4, 4} = 카운트X
최종 1개로 답이 도출된다.
흠.. 일단 검증 같은걸 해보긴 했는데 이걸 검증이라고 할 수 있는지? 모르겠다
||구현
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
set<pii> vertices;
pii operator+(const pii & p1, const pii & p2)
{
return { p1.first + p2.first, p1.second + p2.second };
}
pii operator-(const pii & p1, const pii & p2)
{
return { p1.first - p2.first, p1.second - p2.second };
}
pii Rotate(pii & p)
{
int temp = (p.second * -1);
p.second = p.first;
p.first = temp;
return p;
}
//[0] : 시작 x좌표
//[1] : 시작 y좌표
//[2] : 시작 방향
//[3] : 세대
vector<vector<int>> dcProp;
vector<pii> tdc;
pii moving[4] = { {1, 0},{0, -1},{-1, 0}, {0, 1} };
void MakeDC()
{
//1. 드래곤 커브를 개수만큼 생성한다.
for (const auto & d : dcProp)
{
//1.1 0세대의 시작 좌표 저장
pii s = { d[0], d[1] };
tdc.push_back(s);
//1.2 0세대의 끝점 계산, 좌표 기록
tdc.push_back(s + moving[d[2]]);
//1.3 세대가 성장하는가?
if (0 < d[3])
{
//1.3.1 2세대이상부터, 입력 세대 만큼 커브 성장
for (int i = 1; i <= d[3]; ++i)
{
pii e = tdc.back();
int tempSize = tdc.size();
//이전까지의 꼭짓점 회전 시켜 좌표 기록
for (int j = tempSize - 2; 0 <= j ; --j)
{
pii t = tdc[j] - e;
tdc.push_back(e + Rotate(t));
}
}
}
//최종 저장
for (const auto & d : tdc)
{
vertices.insert(d);
}
tdc.resize(0);
}
}
// (x, y) 형태의 좌표
pii preset[3] = { {1, 0}, {0, 1}, {1, 1} };
int ret = 0;
void CheckRect()
{
//1. 각 꼭짓점 검사
for (auto & d : vertices)
{
bool isRect = true;
for (int i = 0; i < 3 && isRect; ++i)
{
if (vertices.find(d + preset[i]) == vertices.end()) isRect = false;
}
if (isRect == true) ++ret;
}
}
int main()
{
ios::sync_with_stdio(0), cin.tie(0);
int c; cin >> c;
dcProp.resize(c);
for (int i = 0; i < c; ++i)
{
dcProp[i].resize(4);
cin >> dcProp[i][0] >> dcProp[i][1] >> dcProp[i][2] >> dcProp[i][3];
}
MakeDC();
CheckRect();
cout << ret;
return 0;
}||되돌아보기
막힌 부분이 두 부분이 있었다.
1.문제의 조건을 잘못 이해
문제를 풀면서 점점 내가 문제를 이해 완벽히 이해하지 못한다고 생각이 들었다.
코드는 완성했는데 예시의 답과는 다르게 나오고,
조건이 틀렸는지 확인하고, 틀린 조건 수정하고 => 이 단계 반복이 좀 많았다;
문제 조금보고 이해했다고 깝치지말고
다음에는 내가 이해한 것과 예시가 같은지도 제대로 비교해서 문제를 확실히 이해하고 넘어가야겠다😪
2.다양한 예시
내가 0세대에서 1세대로 넘어가는 예시만 생각하는 바람에
끝 좌표 이전의 모든 좌표를 회전시켜서 저장하지 못하고 시작 좌표만 회전시켜서 저장되었다.
너무 많은 예시는 아니더라도 최소 2개정도의 예시를 생각하자
||개선 코드
내 코드에서 일단 가볍게 개선 해봤다.
일단 회전 부분을 (y * -1, x)으로 간단히 했고
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
//[0] : start X //[1] : start Y //[2] : 시작 방향 //[3] : 세대
vector<vector<int>> dcProp;
set<pii> vertices;
vector<pii> tdc;
pii operator+(const pii & p1, const pii & p2)
{
return { p1.first + p2.first, p1.second + p2.second };
}
pii operator-(const pii & p1, const pii & p2)
{
return { p1.first - p2.first, p1.second - p2.second };
}
pii moveSet[4] = { {1, 0},{0, -1},{-1, 0}, {0, 1} };
void MakeDC()
{
//1. 드래곤 커브를 개수만큼 생성한다.
for (const auto & d : dcProp)
{
//1.1 0세대의 시작, 끝 좌표 저장
pii s = { d[0], d[1] };
tdc.push_back(s);
tdc.push_back(s + moveSet[d[2]]);
//1.2 1세대이상부터, 입력 세대 만큼 커브 성장
for (int i = 1; i <= d[3]; ++i)
{
pii e = tdc.back();
int tempSize = tdc.size();
//1.2.1 끝점 이전의 꼭짓점들 회전 시켜 좌표 기록
for (int j = tempSize - 2; 0 <= j ; --j)
{
pii t = tdc[j] - e;
tdc.push_back(e + make_pair(t.second * -1, t.first));
}
}
//최종 저장
for (const auto & d : tdc)
{
vertices.insert(d);
}
tdc.resize(0);
}
}
pii checkSet[3] = { {1, 0}, {0, 1}, {1, 1} };
int CheckRect()
{
int ret = 0;
//저장한 각 꼭짓점 검사
for (auto & d : vertices)
{
bool isRect = true;
for (int i = 0; i < 3 && isRect; ++i)
{
if (vertices.find(d + checkSet[i]) == vertices.end()) isRect = false;
}
if (isRect == true) ++ret;
}
return ret;
}
int main()
{
ios::sync_with_stdio(0), cin.tie(0);
//1. Input values
int c; cin >> c;
dcProp.resize(c);
for (int i = 0; i < c; ++i)
{
dcProp[i].resize(4);
cin >> dcProp[i][0] >> dcProp[i][1] >> dcProp[i][2] >> dcProp[i][3];
}
//2. Do calculate & Print result
MakeDC();
cout << CheckRect();
return 0;
}

'코딩 테스트 > 알고리즘 풀이' 카테고리의 다른 글
| [알고스팟 - TRIANGLEPATH] 삼각형 위의 최대 경로 (0) | 2023.01.08 |
|---|---|
| [알고스팟 - QUADTREE] 쿼드 트리 뒤집기 (0) | 2022.12.10 |
| [백준 - 1620] 나는야 포켓몬 마스터 이다솜 (0) | 2022.12.09 |
| [종만북] 행렬의 거듭제곱 (0) | 2022.12.07 |
| [종만북] 수열의 빠른 합 (0) | 2022.12.06 |
| [알고스팟 - TSP1] Traveling Salesman Problem 1 (0) | 2022.12.04 |
| [백준 - 1560] 비숍 (0) | 2022.12.03 |
| [알고스팟 - PICNIC] 소풍 (0) | 2022.12.02 |

