원인과 결과
베이즈 정리는 한 방향의 조건부 확률을 알고 있을 때, 다른 방향의 조건부 확률을 계산하는 공식입니다.
한 방향은 알고, 한 방향은 모르는 상황이 있을까요?
결과는 알고 원인은 모르는 경우가 해당 상황과 같다고 볼 수 있는데요,
그래서 우리는 결과를 기준으로 원인을 예측해야 하는 상황이 자주 있습니다.
조건부 확률의 수식을 활용하여 나타내면 아래와 같습니다.
- $P(\text{결과} \mid \text{원인})$
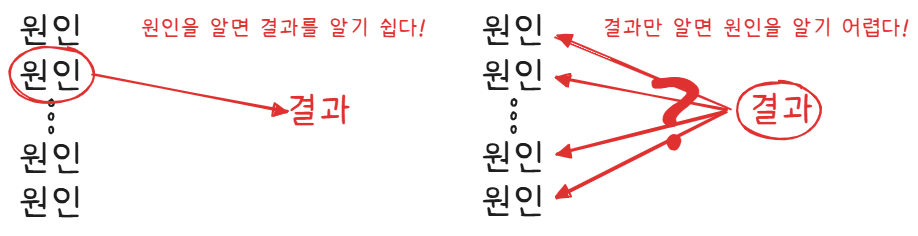
원인을 알고 있을 때, 결과를 예측하는 것은 쉽습니다. - $P(\text{원인} \mid \text{결과})$
결과만 알고 있다면, 원인을 예측하기는 어렵습니다.
예시
- 친구의 문자 답장
$P(\text{결과} \mid \text{원인})$ : 원인이 너무 바쁘다면, 결과로 답장이 없다고 예측이 가능합니다.
$P(\text{원인} \mid \text{결과})$ : 결과로 답장이 없다면, 원인은 다양합니다.(바쁘거나, 폰이 꺼져있거나, … ) - 중고 매물
$P(\text{결과} \mid \text{원인})$ : 원인으로 상태가 더럽다면, 결과로 저렴할 수 있습니다.
$P(\text{원인} \mid \text{결과})$ : 결과가 저렴하다면, 원인은 다양합니다.(하자가 있는지, 사기인지, … )
이처럼, 한 방향의 조건부 확률은 알기 쉽지만, 다른 방향의 조건부 확률을 모르는 경우가 많습니다.
이 상황에 유용하게 사용할 수 있는 정리가 바로 베이즈 정리입니다.
베이즈 정리
한 방향의 조건부 확률을 알고 있을 때, 다른 방향의 조건부 확률을 계산하는 공식입니다.
베이즈 정리 유도
앞선 내용을 이해했다면 유도과정은 어렵지 않습니다.
두 사건 A, B가 존재할 때, $P(B \mid A)$를 이용해 $P(A \mid B)$를 구하는 식을 유도해 봅니다.
베이즈 정리의 유도 과정은 결합확률의 정의에서 출발합니다.
결합확률은 앞에서 배웠듯이 두 가지 방식으로 표현가능합니다.
- $P(A \cap B) = P(A \mid B) \times P(B)$
- $P(A \cap B) = P(B \mid A) \times P(A)$
첫 번째 표현식인 $P(A \cap B) = P(A \mid B) \times P(B)$의 각 항에 $P(B)$를 나누어주면 다음과 같습니다.
$$\dfrac{P(A \cap B)} {P(B)} = P(A \mid B)$$
이때 분자인 $P(A \cap B)$를 위의 첫 번째 표현식을 이용하여 $P(B \mid A) \times P(A)$로 치환한 식이 바로 베이즈 정리입니다.
$$\dfrac{P(B\mid A)\times P(A)} {P(B)} = P(A\mid B)$$
예시
이전글에서 사용했던 예시를 사용하여 베이즈 정리를 활용해 보겠습니다.
여기서 빨간 과일 중 사과일 확률인, $P(\text{사과}\mid\text{빨간 과일})$을 구하겠습니다.
| 구분 | 개수 |
| 전체 과일 | 100개 |
| 사과 | 40개 |
| 빨간 과일 | 15개 |
| 빨간 사과 | 10개 |
근데, 이렇게 데이터가 많이 제공되어, 결합 확률과 전체 분포를 알고 있다면 사실 암산으로도 구할 수 있습니다..
그래서 보통 $P(\text{A}\mid\text{B})$을 예측할 때, $P(B)$와 $P(\text{B}\mid\text{A})$만 알고 있는 상황이 많은데요,
해당 상황에 맞는 표는 아래와 같습니다.
| 구분 | 확률 |
| 사과 | 0.4 (40%) |
| 사과 중 빨간 비율 | 0.25 (25%) |
| 사과가 아닌 과일 중 빨간 비율 | 0.083 (8.3%) |
| 빨간 과일중 사과 (조건부 확률 B) |
구하고 싶은 값 |
데이터의 단위가 개수에서 확률로 변경됐는데, 같은 값을 다르게 표현한 것뿐입니다.
왜냐하면 베이즈 정리는 숫자의 크기가 아니라 비율 관계만 필요하기 때문입니다.
베이즈 정리를 이용하면 다음과 같습니다.
$$P(\text{사과}\mid\text{빨간 과일})=\dfrac{P(\text{빨간 과일}\mid\text{사과})\times P(\text{사과})}{P(\text{빨간 과일})}$$
해당 식에서 우리는 분자는 알지만, 분모인 $P(\text{빨간 과일})$는 아직 알 수 없습니다.
이때 사용하는 것이 전체 확률의 법칙인데, 해당 개념은 다음 글에서 정리해 보겠습니다.
전체 확률의 법칙을 이용하면 $P(\text{빨간 과일})$은 0.15가 나오게 되는데요,
분모까지 구했으니 베이즈 정리를 이용하여 $P(사과\mid빨간 과일)을 구하는 과정은 아래와 같습니다.
$$=\dfrac{0.25 \times 0.4}{0.15}$$
$$=\dfrac{0.1}{0.15}$$
$$= 0.66\overline{6} \approx 67\%$$
즉, 빨간 과일을 하나 집었을 때, 그게 사과일 확률은 67%라고 예측할 수 있습니다.
실제로도 빨간 과일이 15개고, 사과는 그중 10개이므로 비율이 $10/15 = 25%$가 되어,
베이즈 정리의 계산 값과 정확히 일치하는 것을 알 수 있습니다.
마무리하며
처음 우리가 아무 정보 없이 100개의 과일 바구니를 봤을 때, 사과를 집을 확률은 40%였습니다.
하지만 빨간 과일이라는 새로운 정보가 추가되는 순간, 확률이 67%까지 올라갔습니다.
마치 게임에서 빨간 과일 태그를 가진 아이템만 남기고 나머지는 필터링해서 화면에서 치워버리는 것과 같습니다.
100개였던 후보가 순식간에 15개로 압축되고, 그 작은 바구니 안에는 사과가 무려 10개나 들어있게 되죠.
이처럼 후보군이 좁혀지면서 내가 원하는 결과의 비중이 커지는 것, 이것이 바로 베이즈 정리의 핵심이라고 생각합니다.
이 각 확률은 수학에서 이렇게 표현됩니다.
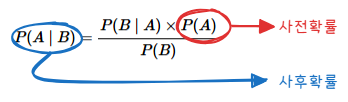
- 정보가 없을 때의 확률(40%)을 사전 확률
- 정보를 통해 필터링된 확률(67%)을 사후 확률
결국 베이즈 정리는 새로운 정보를 수집할 때마다 우리의 예측을 더 정교하게 업데이트해 나가는 과정이라고 생각합니다.

