[종만북] 행렬의 거듭제곱
||문제 이해
자연수 m이 주어질 때, 행렬^m 을 구하라
||해결 계획
분할 정복을 사용한다.
1. 먼저 재귀의 초기형을 짜본다.
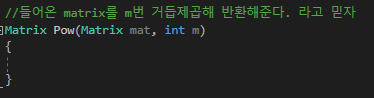
2. 그리고 m이 짝수일 경우와 홀수일 경우가 다른데 일단 짝수로 생각해보자
행렬의 짝수 거듭제곱인 A^4를 풀어보면 이렇다.
A^4 = A * A * A * A
이 식은 행렬 A의 4거듭제곱이니 Pow(A, 4)와 같다!
곱셈은 자리를 변경해도, 어떤것부터 곱하던지 값은 항상 똑같기에 분할하기 편하게 반으로 나누어보자
A^4 = (A * A) * (A * A) = A^2 * A^2
이렇게 되면 저 하나의 A^2는 Pow(A,2)로도 가능하다!
즉, A^4 = Pow(A, 2) * Pow(A, 2) 이다.
그럼 최종의 최종은 Pow(A,4) = Pow(A, 2) * Pow(A, 2) 일 것이다.

하지만 이렇게 되면 사실 분할정복의 의미가 없다.
분할정복을 정리하면서 깨달은건데
큰 그림만 놓고보면 사실 일반 재귀와 분할정복의 재귀 호출 수는 똑같다.

하나의 뭉텅이가 재귀 한번인데 각 개수를 세보면 11개로 똑같다.
근데 이 문제에서의 분할 정복이 메리트가 있는 건
※모든 분할정복이 그렇다는 건 아님
분할했을 때 A뭉텅이, B뭉텅이가 나온다고 하면
A뭉텅이의 재귀 값으로 B뭉텅이를 재귀호출하지 않고 알 수 있어서가 아닐까 싶다.
암튼 지금까지 경험상은 그렇다.
그래서 분할정복을 사용하려면 코드는 이렇게 되어야한다.

3. 이제 짝수는 되었으니 간단한 홀수를 추가한다.
A^5 = A * A^4 인건 당연한 사실
즉, A * Pow(A, A-1)로 홀수거듭제곱을 알 수 있다.

4. Base case를 추가해주면 완성이다.

||구현
Matrix Pow(Matrix mat, int m)
{
//base case, 최소의 부분문제이므로 m이 1일때이다.
if (m == 1) return mat;
//홀수일 때의 답 반환
if (m & 0x1) return mat * Pow(mat, m - 1);
//m이 짝수일 때의 답 반환
Matrix half = Pow(mat, m / 2);
return half * 2;
}||되돌아보기
책에서는 홀수일때 다른 방법도 제시했는데
pow(A, m/2) * pow(A, m/2 + 1) 이다.
내가 작성한 짝수일때 pow(A, m/2) * pow(A, m/2)와 같은 경우다.
이것도 마찬가지로 재귀호출양이 훨씬 많다.
하지만 이 방식이 더 빠르게 답을 도출하는 방법이 있는데
바로 동적계획법(DP)이다.
근데 이말을 듣고 생각해보니까 분할하는 여러 방법이 있겠다 싶었다.
그래서 무조건 반이아닌 좀 더 효율적인 분할방법을 찾아보려고도 해야겠다!
dp는 아직 내가 자신있게 풀수있는건 아니여서 얼른 속도내서 뒷장에서 공부해야겠다 = ~ =
암튼 이번 문제를 정리하면서 분할정복이 왜 재귀와 차이가 나는지 깨달았다.
이렇게 좀 논리적인 코드를 작성하려고 노력하다보니까 예전보다 재귀 작성하기가 쉬워졌고
앞으로도 항상 더 논리적인 코드를 짜려고 노력해야겠다.