코딩 테스트/알고리즘 풀이
[백준 - 1074] Z
김띠띵
2022. 8. 26. 16:58
#include <iostream>
using namespace std;
typedef long long int ll;
int pre[16] = { 1,2,4,8,16,32,64,128,256,512,1024,2048,4096,8192,16384,32768 };
//0 : 좌측상단 , 1 : 우측상단, 2 : 좌측하단, 3 : 우측하단
int GetQuadrant(const bool & X, const bool & Y)
{
if (X == true)
{
if (Y == true) return 3;
else return 1;
}
else
{
if (Y == true) return 2;
else return 0;
}
}
ll Func(ll N, ll X, ll Y)
{
if (N == 0) return 0;
//사분면 알아내기
ll mid = pre[N] / 2;
ll q = GetQuadrant(mid <= X, mid <= Y);
//자기사각형에서의 최대값
ll std = pre[N - 1] * pre[N - 1];
ll max = std * q;
//값 합쳐 반환
return max + Func(N - 1, X % mid, Y % mid);
}
int main()
{
ios::sync_with_stdio(0), cin.tie(0);
ll N, Y, X; cin >> N >> Y >> X;
cout << Func(N, X, Y);
return 0;
}||사고 과정
처음엔 진짜 뭔가 싶었던 1시간 5분 소요해서 풀은 문제...
일단 처음에 함수 형태를 생각했다.
int func(int n, int x, int y)
{
return "x와 y좌표에 속하는 번호"
}그리고 규칙을 찾았다.
처음엔 가로 몇번째 줄은 * 2하고 +2를 하고.. 세로는 뭐 어쩌구저쩌구 규칙이 있을까 하면서 생각했다.
그러던 중에 사각형이 4개 뭉텅이로 보이고 각 첫 숫자들이 보이게 됐다.
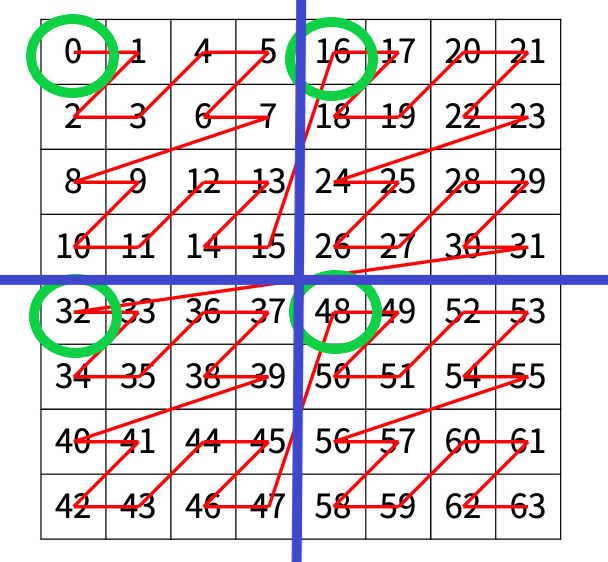
오 이렇게 16씩 더해지네 하다가 정말 기적처럼 결정적인 아이디어가 생각났다.
속한 사분면에 들어가서 다시 사분면으로 나누고 다시 사분면으로 나누고... 재귀적 아이디어였다.
예를 들어 밑의 별표는 저런식으로 4분면을 쪼개어 들어가는 것이였다.

그렇게 생각하게 된 함수는 이런식으로 변경했다.
int func(int n, int x, int y)
{
return "2^n * 2^n인 사각형에서 최대로 가질수 있는 수"
}이걸 생각하고 나서 문제 진행이 수월해졌고
이걸 재귀적으로 다시 수정하면
int func(int n, int x, int y)
{
if(n == 0) return 0;
return "2^n * 2^n인 사각형에서 최대로 가질수 있는 수" + func (n - 1, x, y)
}이러면 한 변이 2^n인 사각형에서 구할 수 있는 최대 수 + 2^n-1인 사각형에서 구할 수 있는 최대 수 ...
이런식으로 나오기 때문에 답을 구할 수 있겠다고 생각했다.
||사용 기법
- Recursive
||풀면서 느낀 것
- 모르겠을 때는 가만히 있지말고 뭐라도 해라
정말 이것저것 그리거나 규칙을 찾으려고 하지 않았으면 재귀적 아이디어도 떠오르지 않았을 것이다.
||나아 진것
- 재귀적 아이디어를 잘 찾은 것
재귀 문제를 많이 풀어보지 않았는데 혼자 이렇게 생각해 낸것에 대해 약간 뿌듯할지도...😎